Realtime visualization of 3D vector fields using CUDA
Chapter 6: Performance benchmark
The most figures in this report were computed at interactive frame rates.
The biggest limitation of CUDA approach is GPU memory.
Raw data itself consumed about 1.5 GB leaving about 2 GB for geometry.
The application has parameter called geometry sampling which significantly lowers
memory needed for geometry without losing integrator's precision.
Value of this parameter means how many samples of integrator to compute per sample of output geometry.
Another problem with memory is that all memory needs to be allocated before GPU kernel is invoked. This means that for every thread (potential line) there must be enough space no matter how long each stream line will be. If line integration will stop in the middle there will be half of that line's memory unused.
In order to benchmark this application, time step was set to unnecessary low values and number of primitives to ridiculous values.
Hardware
Hardware matters since the solution is heavily using CUDA. Following hardware was used to create all figures in this report.
- OS: MS Windows 7 Enterprise 64-bit SP1
- CPU: Intel Core i7 920 @ 2.67GHz
- RAM: 12.0 GB Triple-Channel DDR3 @ 531MHz
-
GPU: NVIDIA Quadro K5000, 4096 MB GDDR5
- CUDA Driver Version: 5.0
- CUDA Capability: 3.0 (program needs at least 2.0)
- 8 Multiprocessors x 192 CUDA Cores/MP: 1536 CUDA Cores
Comparison of Euler and RK4 integrators
As discussed in Chapter 3: Vector field integrators for stream line visualization, I've implemented two different integrators.
First was implemented Euler's integrator because I thought that GPU is fast enough
and smaller time step will ensure good precision.
In the middle of the project, one friend (math major) told me that RK4 would do much better than Euler
no matter the time step.
For those who understand O-notation, Euler's integrator have error O(dt2)
and RK4 O(dt5) where dt is time step (dt << 1).
I did not believe them, so I implemented RK4 and compared results.
After comparing results visually (see Figure 19), I had to admit that my friend was right. Euler tends to escape vortices even for very low time step values but RK4 does much better job. Interestingly enough, RK4 sometimes converge to the center of vortices instead of escaping them. I did not perform any measurement of the error because the visuals were enough for me to admit that RK4 does much better job than Euler.

Euler integrator for dt=2^-12 
RK4 integrator for dt=2^-12 
Euler integrator for dt=2^-10 
RK4 integrator for dt=2^-10 
Euler integrator for dt=2^-8 
RK4 integrator for dt=2^-8 
Euler integrator for dt=2^-6 
RK4 integrator for dt=2^-6 
Euler integrator for dt=2^-4 
RK4 integrator for dt=2^-4 
Euler integrator for dt=2^-3 
RK4 integrator for dt=2^-3
Glyphs
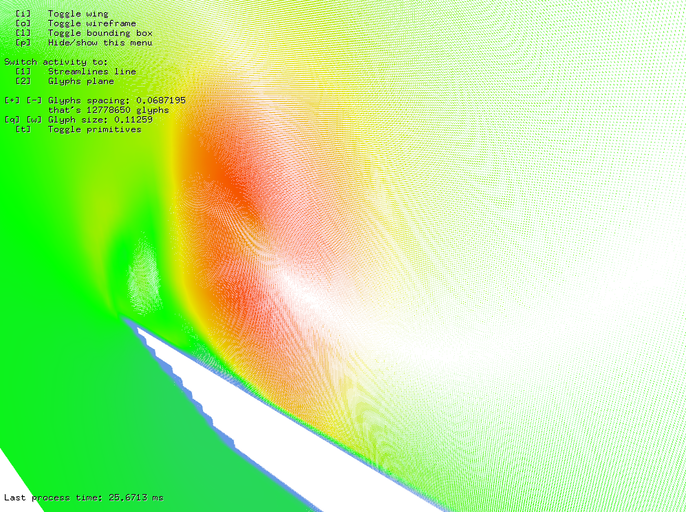
The first benchmark was done with glyph lines. Since every line requires only one query to vector field, the number of lines literally do not matter at all. The only limit is GPU memory and every line takes very few of it as well. This means that the application is capable to render a huge amount of line glyphs at once forming. Figure 20 shows that nearly 13 million of glyphs were computed in mere 26 ms. The density of glyph lines is so high that you can even see individual voxels of data near edge of wing.
I did benchmark with arrow glyphs as well but the result was just bog blob of arrows and it was hard to see anything so I decided to not put the image here.
Stream lines and tubes
The second benchmark was dealing with stream lines. 215 stream lines for 212 steps took 183 ms and 216 steam lines took 207 ms. In this point the interactivity is not that great but 216 stream lines is just crazy number anyway. Just for curiosity, 216 stream lines for 216 steps took a little more than 8 seconds. For this test I had to override default time Windows that waits to display driver to respond before they restart it (default was 3 seconds).

215 stream lines for 212 steps took 183 ms. 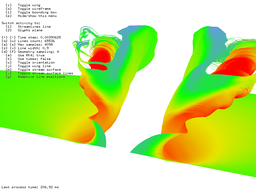
216 stream lines for 212 steps took 207 ms. 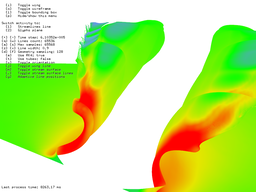
216 stream lines for 216 steps took 8 s.
The third benchmark uses adaptive algorithm for computing stream lines. As you can see in Figure 22 it is roughly three-times slower computing 215 stream lines for 212 steps in 450 ms. However if you take into account that adaptive algorithm is counted in iterative manner on GPU and CPU, the result is surprisingly fast.
Unfortunately, adaptive algorithm does not work with stream tubes. There is a bug that stream lines are all over the place - some array indices gets messed up while counting adaptive algorithm and I had no time to fix it.
Next benchmark was testing stream tubes. Computation power needed for integration of stream tubes is the same as for stream lines but stream tubes has much more vertices and the kernel also computes indices for faces and normals which makes them heavy for memory writing and consumes much more overall GPU memory. Figure 23 shows that 213 stream tubes of 213 samples took 240 ms.
Stream surface
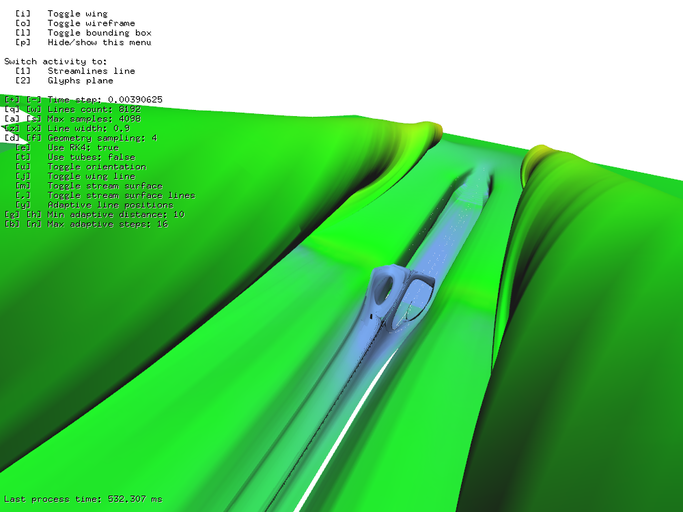
The last test is testing adaptive stream surface algorithm. Figure 24 shows 213 seeds for 212 steps using adaptive stream surface algorithm took 532 ms.
Because of the adaptivity of the algorithm total time depends on the origin of the stream surface. However, my goal was not to do scientifically precise proof but just to estimate what is my system capable of.
Extra
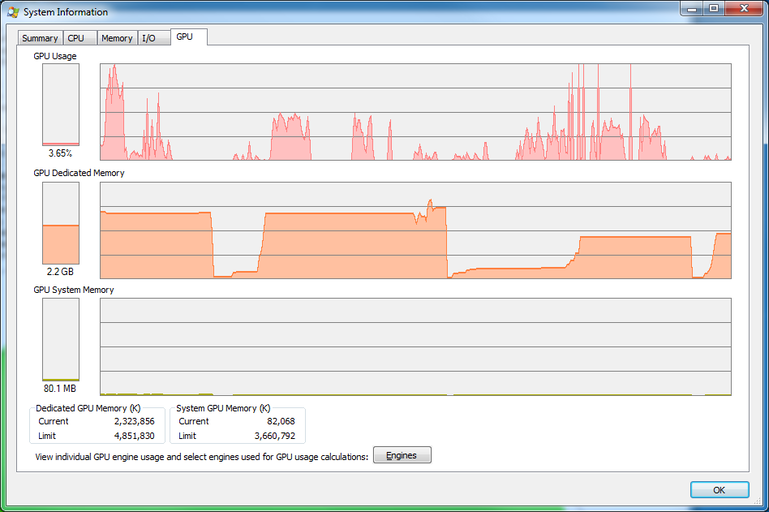
Lastly, Figure 25 shows SysInternal's Process Manger GPU card while I was playing with the program. GPU is not 100% utilized because there is always some spare time between CUDA individual computations.
It was quite interesting to observe how Operating system and nVidia drivers handle situations when GPU is out of memory. Sometimes, part of GPU memory was swapped and "GPU System Memory" graph rose. Unfortunately, usually application just failed to allocate GPU memory. I was not able to achieve any stable results.