Conway's Game of Life on GPU using CUDA
Chapter 4: Advanced implementation: lookup table
The results from previous Chapter 3: Advanced implementation: 1 bit per cell were very nice, speedups reaching up to 480× over the basic serial CPU implementation. However, I was hoping to reach even higher speedups by implementing a lookup table evaluation. The problem with the bit counting is that it is quite computation heavy. The GPU has to perform more than a hundred arithmetic operations in order to evaluate a single byte of data.
Instead of counting of neighbors, the state of cells could be easily encoded into a number and lookup table could be used to evaluate it.
The problem is that the size of potential lookup table is exponential with the size of the state; 2state cells count to be exact.
Finding optimal evaluation area
A 3×3 area is needed of cells is needed in order to evaluate a single cell. It would take 8 lookups to evaluate whole byte of data. If two cells would be evaluated at once, only four lookups would be needed but table would have to be constructed for area of 4×3 cells.
The goal is to compromise between size of the table and number of evaluated cells at once.
The shape of evaluated area also makes difference. Ratio between number of evaluated cells and their neighborhood necessary for their evaluation is the best for square-ish shapes. Data are, however, stored in rows, it is much easier to read a row than a column. This is the reason why only considered areas have 3 rows. There might be some benefit of reading more than 3 rows but I did not go that way.
Figure 15 summarizes all the important factors of several cell configurations.
The table nicely shows how larger areas are more effective but they need to have much larger lookup table. Small lookup table helps the performance because it can fit into the processor's caches, which is extremely important. Reading from caches is much faster than from main memory. All sizes of evaluated cells are powers of two to be able to align them to 8-bit bytes.
I did not have time to write the code for all options and do the performance analysis so I wanted to do educated guess what would be the best option. I really liked the 3×10 option because that one would allow me to work with whole bytes (result is 8 bits — one byte). However, 1 GB lookup table is insane, especially for GPU with a few GB's of available memory.
Long story short, due to many implementation details and lookup table size I decided to use the 6×3 area.
| Size | Eval. cells per step | Eval. steps | Lookup table rows | Lookup table size (optimal) | Lookup table size (byte per row) |
|---|---|---|---|---|---|
| 3×3 | 1 | 8 | 29 = 512 |
29 ∙ 1 b = 64 B |
29 ∙ 8 b = 512 B |
| 4×3 | 2 | 4 | 212 = 4096 |
212 ∙ 2 b = 1 KB |
212 ∙ 8 b = 4 KB |
| 6×3 | 4 | 2 | 218 = 262144 |
218 ∙ 4 b = 128 kB |
218 ∙ 8 b = 256 kB |
| 3×10 | 8 | 1 | 230 ≈ 1 bil |
230 ∙ 8 b = 1 GB |
230 ∙ 8 b = 1 GB |
Lookup table construction
I decided to use a lookup table for area 6×3 which means that the lookup table has to have 26∙3 = 218 rows.
The values in this table have 4 bits which makes the table 218 ∙ 4 b = 128 kB big.
The optimal sized table has two entries in every byte which makes access complicated.
I decided to use sub-optimal solution storing every entry in a byte (not in 4 bits) which makes the table twice as big.
The lookup table is computed by the GPU.
Code listing 11 shows the kernel which is invoked on 218 threads (256 threads per block on 1024 blocks).
The computation itself is pretty straight forward. Every table index represents 6×3 area of cells. Value on that index represents result state of 4 middle cells. The kernel computes just that and saves it to given array.
Helper function getCellState serves to get the bit in coordinates x and y in given 6×3 area of given key key
The lookup table is computed only once per program lifetime and it is kept in the GPU memory all the time. The table takes only 256 KB of GPU memory which is negligible. There is no need for analyzing of computation performance or for trying to make the computation faster. The fact that it is implemented using CUDA is already overkill.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
__global__ void precompute6x3EvaluationTableKernel(ubyte* resultEvalTableData) {
uint tableIndex = __mul24(blockIdx.x, blockDim.x) + threadIdx.x;
ubyte resultState = 0;
// For each cell.
for (uint dx = 0; dx < 4; ++dx) {
// Count alive neighbors.
uint aliveCount = 0;
for (uint x = 0; x < 3; ++x) {
for (uint y = 0; y < 3; ++y) {
aliveCount += getCellState(x + dx, y, tableIndex);
}
}
uint centerState = getCellState(1 + dx, 1, tableIndex);
aliveCount -= centerState; // Do not count center cell in the sum.
if (aliveCount == 3 || (aliveCount == 2 && centerState == 1)) {
resultState |= 1 << (3 - dx);
}
}
resultEvalTableData[tableIndex] = resultState;
}
inline __device__ uint getCellState(uint x, uint y, uint key) {
uint index = y * 6 + x;
return (key >> ((3 * 6 - 1) - index)) & 0x1;
}
GPU implementation
The CUDA kernel for implementation of described lookup table evaluation algorithm is shown in Code listing 12. The code is very similar to previous bit-counting technique described in Chapter 3: Advanced implementation: 1 bit per cell.
The major difference is in the evaluation itself. Instead of a cycle that counts bits, encoding of life state is performed and the lookup table is used for evaluation.
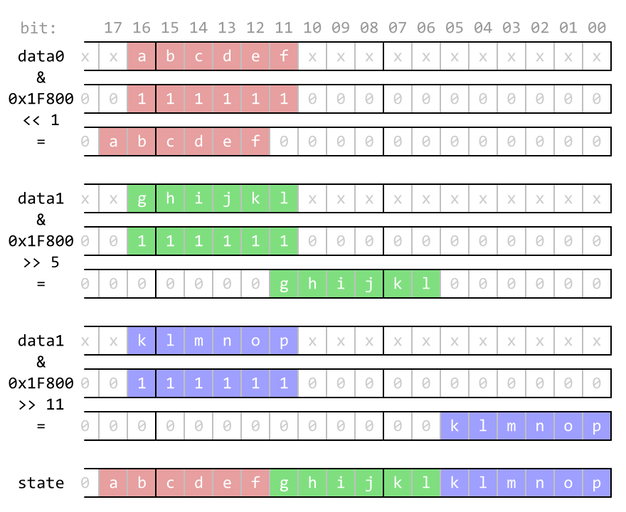
In order to evaluate a whole byte, two lookups are needed. Figure 16 and following code snippet shows the code for encoding the cell states.
1
2
uint lifeStateHi = ((data0 & 0x1F800) << 1) | ((data1 & 0x1F800) >> 5) | ((data2 & 0x1F800) >> 11);
uint lifeStateLo = ((data0 & 0x1F80) << 5) | ((data1 & 0x1F80) >> 1) | ((data2 & 0x1F80) >> 7);
The evaluation using lookup table is as simple as the last line in Code listing 12.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
__global__ void bitLifeKernel(const ubyte* lifeData, uint worldDataWidth,
uint worldHeight, uint bytesPerThread, const ubyte* evalTableData,
ubyte* resultLifeData) {
uint worldSize = (worldDataWidth * worldHeight);
for (uint cellId = (__mul24(blockIdx.x, blockDim.x) + threadIdx.x) * bytesPerThread;
cellId < worldSize;
cellId += blockDim.x * gridDim.x * bytesPerThread) {
uint x = (cellId + worldDataWidth - 1) % worldDataWidth; // start at block x - 1
uint yAbs = (cellId / worldDataWidth) * worldDataWidth;
uint yAbsUp = (yAbs + worldSize - worldDataWidth) % worldSize;
uint yAbsDown = (yAbs + worldDataWidth) % worldSize;
// Initialize data with previous byte and current byte.
uint data0 = (uint)lifeData[x + yAbsUp] << 8;
uint data1 = (uint)lifeData[x + yAbs] << 8;
uint data2 = (uint)lifeData[x + yAbsDown] << 8;
x = (x + 1) % worldDataWidth;
data0 |= (uint)lifeData[x + yAbsUp];
data1 |= (uint)lifeData[x + yAbs];
data2 |= (uint)lifeData[x + yAbsDown];
for (uint i = 0; i < bytesPerThread; ++i) {
uint oldX = x; // Old x is referring to current center cell.
x = (x + 1) % worldDataWidth;
data0 = (data0 << 8) | (uint)lifeData[x + yAbsUp];
data1 = (data1 << 8) | (uint)lifeData[x + yAbs];
data2 = (data2 << 8) | (uint)lifeData[x + yAbsDown];
uint lifeStateHi = ((data0 & 0x1F800) << 1) | ((data1 & 0x1F800) >> 5) | ((data2 & 0x1F800) >> 11);
uint lifeStateLo = ((data0 & 0x1F80) << 5) | ((data1 & 0x1F80) >> 1) | ((data2 & 0x1F80) >> 7);
resultLifeData[oldX + yAbs] = (evalTableData[lifeStateHi] << 4) | evalTableData[lifeStateLo];
}
}
}
Bit life kernels invocation
Invocation of all bit-life CUDA kernels is done by single methods shown in Code listing 13. There are three different kernels: bit counting, bit counting on big chunks and lookup table.
The first half of the code is full of checks of proper alignment and size of the world based on given parameters. The parameters make a lot of restriction on the actual world dimensions but honestly I do not think it would be worth the effort to make it work for any world size.
Then, total number of needed CUDA blocks is computed based on the total number of cells and given parameters.
You might notice that the amount of actual blocks is clamped to 32768 (215).
If there are more blocks needed, every thread will process more chunks.
This is achieved by a big for-cycle surrounding whole kernel.
The last part of the code is invocation of a right kernel based on the parameters.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
bool runBitLifeKernel(ubyte*& d_encodedLifeData, ubyte*& d_encodedlifeDataBuffer,
const ubyte* d_lookupTable, size_t worldWidth, size_t worldHeight,
size_t iterationsCount, ushort threadsCount, uint bytesPerThread,
bool useBigChunks) {
// World has to fit into 8 bits of every byte exactly.
if (worldWidth % 8 != 0) {
return false;
}
size_t worldEncDataWidth = worldWidth / 8;
if (d_lookupTable == nullptr && useBigChunks) {
size_t factor = sizeof(uint) / sizeof(ubyte);
if (factor != 4) {
return false;
}
if (worldEncDataWidth % factor != 0) {
return false;
}
worldEncDataWidth /= factor;
}
if (worldEncDataWidth % bytesPerThread != 0) {
return false;
}
size_t encWorldSize = worldEncDataWidth * worldHeight;
if ((encWorldSize / bytesPerThread) % threadsCount != 0) {
return false;
}
size_t reqBlocksCount = (encWorldSize / bytesPerThread) / threadsCount;
ushort blocksCount = (ushort)std::min((size_t)32768, reqBlocksCount);
if (d_lookupTable == nullptr) {
if (useBigChunks) {
uint*& data = (uint*&)d_encodedLifeData;
uint*& result = (uint*&)d_encodedlifeDataBuffer;
for (size_t i = 0; i < iterationsCount; ++i) {
bitLifeKernelCountingBigChunks<<<blocksCount, threadsCount>>>(data,
uint(worldEncDataWidth), uint(worldHeight), bytesPerThread, result);
std::swap(data, result);
}
}
else {
for (size_t i = 0; i < iterationsCount; ++i) {
bitLifeKernelCounting<<<blocksCount, threadsCount>>>(d_encodedLifeData,
uint(worldEncDataWidth), uint(worldHeight), bytesPerThread,
d_encodedlifeDataBuffer);
std::swap(d_encodedLifeData, d_encodedlifeDataBuffer);
}
}
}
else {
for (size_t i = 0; i < iterationsCount; ++i) {
bitLifeKernelLookup<<<blocksCount, threadsCount>>>(d_encodedLifeData,
uint(worldEncDataWidth), uint(worldHeight), bytesPerThread, d_lookupTable,
d_encodedlifeDataBuffer);
std::swap(d_encodedLifeData, d_encodedlifeDataBuffer);
}
}
checkCudaErrors(cudaDeviceSynchronize());
return true;
}
CPU implementation and performance evaluation
The CPU implementation of lookup table technique is nearly identical to the GPU implementation. Actual implementation can be found on GitHub.
Evaluation speeds of the CPU implementation for different values of consecutive evaluated blocks (cb) are shown in Figure 17. The more cb the better evaluation speeds. I could have run the benchmark for more bpt values but unfortunately I did not have time to do that.
Interesting data are presented by Figure 18 where speedups are shown for all CPU implementations described so far over the basic serial CPU.
GPU performance evaluation
The GPU implementation of lookup table technique has two parameters: number of consecutively evaluated blocks (cb) and threads per CUDA block (tpb). It would be appropriate to construct 3D graph but to make it simple, the GPU was performing the best for 512 threads per block. Figure 19 shows evaluation speeds for 512 tpb and varying number of cb compared to the basic GPU implementation. The speedup is not very large, just about two times.
Figure 20 shows speedups over the basic serial CPU for all GPU implementations.
This is interesting result. It is probably caused by many more threads and smaller caches on the GPU.
CPU vs. GPU
The last thing in this chapter is comparison of the CPU and GPU performance. Figure 21 shows speedups of the lookup and bit counting algorithms for both CPU and GPU.
The lookup algorithm on the GPU is reaching speedups of 450× which is comparable to 480× of the bit counting algorithm. On the other hand, the lookup implementation on the CPU is about 5× faster than the bit counting reaching speedup of 60× over the serial CPU.
Next chapter talks about visualization of the life on the screen that uses OpenGL and CUDA interoperability to avoid CPU-GPU data transfer. Comparison of all algorithms together is presented in Chapter 6: Conclusion.